Logistic regression is used for binary classification tasks. It models the probability that a given input belongs to a particular class using the logistic function.
From Linear¶
Check the Linear Regression section’s last part.
From Polynomial¶
Let’s take the function from our previous polynomial regression example and convert it into a binary classification problem. We’ll classify points as belonging to class 1 if the output is greater than a certain threshold, and class 0 otherwise.
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
x = np.random.rand(100,1)
y = 3 * x**4 - 7 * x**3 + 2 * x**2 + 11 + np.random.rand(100,1)
# m0 x4 + m1 x3 + m2 x2 + m3 x + m4
def gd(x, y, m0=0, m1=0, m2=0, m3=0, m4=0, epoch=10000, learn=0.001):
n = len(x)
for i in range(epoch):
y_n = m0 * x**4 + m1 * x**3 + m2 * x**2 + m3 * x + m4
m4_l = - 2 / n * np.sum(y - y_n)
m3_l = - 2 / n * np.sum((y - y_n) * x)
m2_l = - 2 / n * np.sum((y - y_n) * x**2)
m1_l = - 2 / n * np.sum((y - y_n) * x**3)
m0_l = - 2 / n * np.sum((y - y_n) * x**4)
m4 = m4 - learn * m4_l
m3 = m3 - learn * m3_l
m2 = m2 - learn * m2_l
m1 = m1 - learn * m1_l
m0 = m0 - learn * m0_l
return m0, m1, m2, m3, m4
m0, m1, m2, m3, m4 = gd(x, y)
print(gd(x, y))
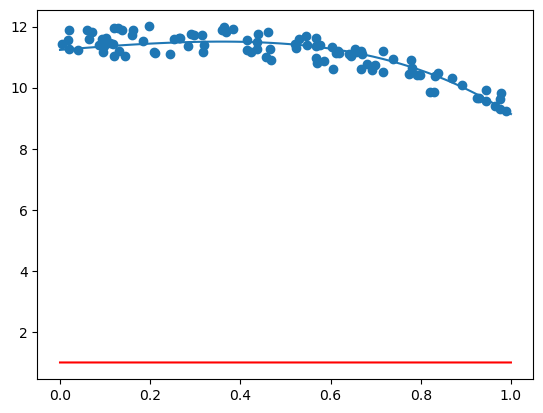
x_p = np.linspace(0, 1)
plt.plot(x_p, m0 * x_p**4 + m1 * x_p**3 + m2 * x_p**2 + m3 * x_p + m4)
plt.scatter(x,y)(np.float64(-1.4008617749474424), np.float64(-1.237676294880945), np.float64(-0.689765797956417), np.float64(1.228140471950126), np.float64(11.237160966215388))
Let’s implement logistic based on the above function.
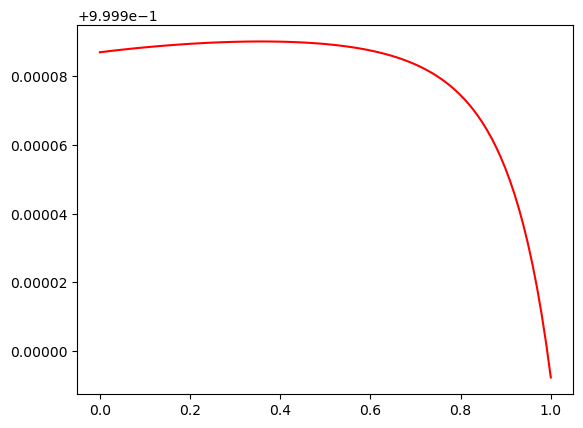
def logistic(z):
return 1 / (1 + np.exp(-z))
def predict(x, m0, m1, m2, m3, m4, threshold=0.5):
z = m0 * x**4 + m1 * x**3 + m2 * x**2 + m3 * x + m4
return logistic(z)
x = np.linspace(0, 1, 100).reshape(-1, 1)
plt.plot(x, predict(x, m0, m1, m2, m3, m4), color='red')