Minimum Spanning Tree
Minimum Spanning Tree (MST)
A spanning tree is defined as a tree-like subgraph of a connected, undirected graph that includes all the vertices of the graph. Or, to say in Layman’s words, it is a subset of the edges of the graph that forms a tree (acyclic) where every node of the graph is a part of the tree.
The minimum spanning tree has all the properties of a spanning tree, with an added constraint of having the minimum possible weights among all possible spanning trees. Like a spanning tree, there can also be many possible MSTs for a graph.
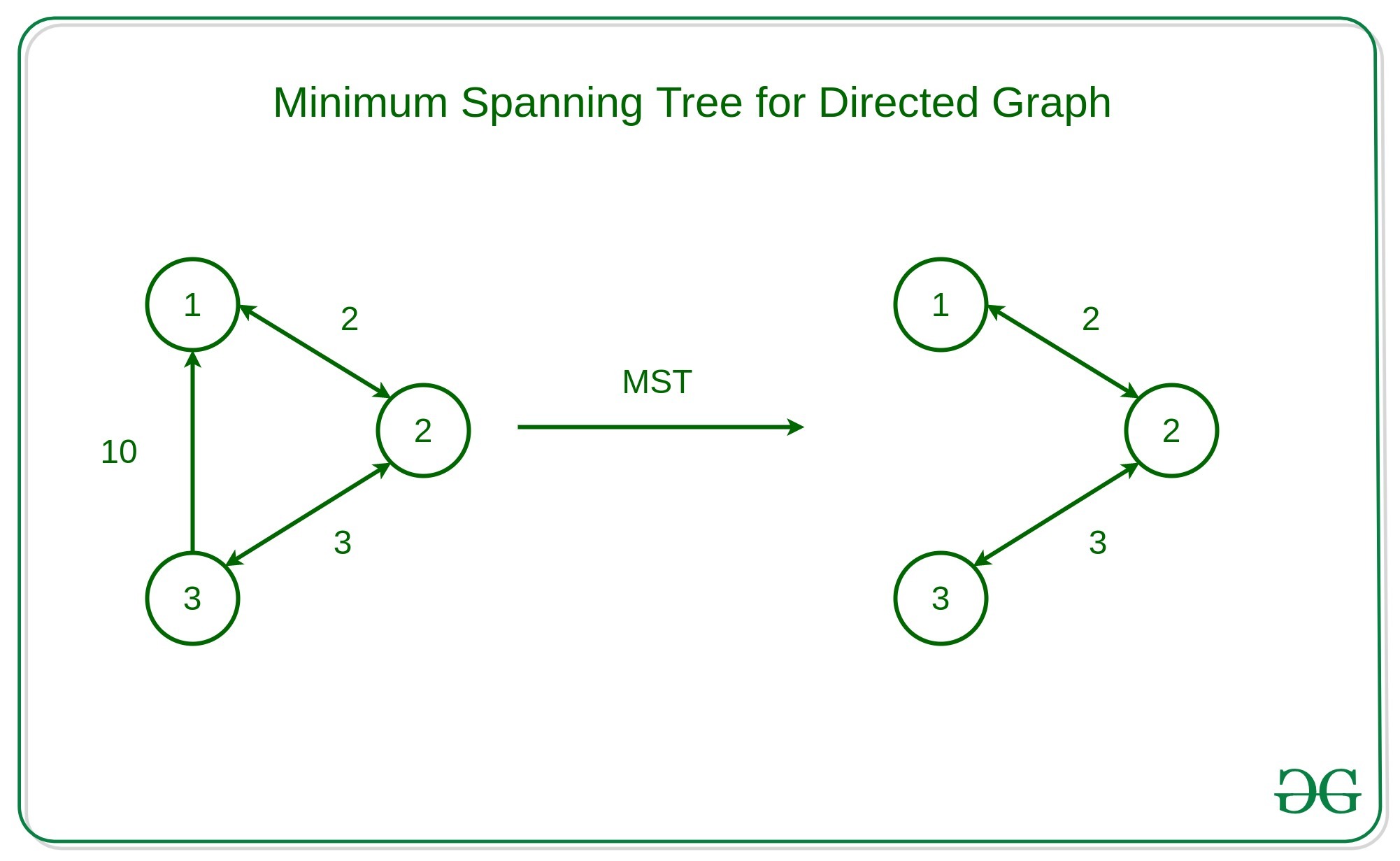
Above texts are taken from Geek for geeks
Now, let's dive deeper with two different algorithms for getting your MST 🙃.
Kruskals
Disjoint Set
Before kruskals let's consider disjoint sets. More information is available here,
{% embed url="https://www.geeksforgeeks.org/introduction-to-disjoint-set-data-structure-or-union-find-algorithm/" %} Disjoint sets {% endembed %}
Here, we are separating each set from other by setting a root for a certain part.
#include <bits/stdc++.h>
using namespace std;
int parent[INT_MAX];
void makeSet(int n) {
for (int i = 0; i <= n; i++)
parent[i] = i;
}
int find(int n) {
if (parent[n] == n) return n;
int result = find(parent[n]);
parent[n] = result;
return result;
}
void unite(int i, int j) {
parent[find(i)] = find(j);
}
int main() {
makeSet(1e6);
unite(1024, 2048);
unite(2048, 4096);
cout << find(1024) << endl;
cout << find(2048) << endl;
cout << find(4096) << endl;
return 0;
}
Actual kruskal
If you have the disjoint, you can sort your data and use the set to do the MST!
#include <bits/stdc++.h>
using namespace std;
vector<pair<int, pair<int, int>>> edges;
int parent[INT_MAX];
void makeSet(int n) {
for (int i = 0; i <= n; i++)
parent[i] = i;
}
int find(int n) {
if (parent[n] == n) return n;
int result = find(parent[n]);
parent[n] = result;
return result;
}
void unite(int i, int j) {
parent[find(i)] = find(j);
}
void addEdges(int i, int j, int k) {
edges.push_back({k, {i, j}});
}
void kruskal() {
sort(edges.begin(), edges.end());
int weight = 0;
for (auto it: edges) {
int i = it.second.first;
int j = it.second.second;
int k = it.first;
if (find(i) != find(j)) {
unite(i, j);
cout << i << " " << j << " " << k << endl;
weight += k;
}
}
cout << "Weight: " << weight << endl;
}
int main() {
makeSet(1e6);
addEdges(0, 1, 10);
addEdges(1, 3, 15);
addEdges(2, 3, 4);
addEdges(2, 0, 6);
addEdges(0, 3, 5);
kruskal();
return 0;
}
Prim
Adjacency matrix
For prim, you can do with adjacency list without any priority queue,
#include<bits/stdc++.h>
using namespace std;
vector<vector<int>> graph;
int V = 5;
void printMST(vector<int> &parent);
int minimum(vector<int> &key, vector<bool> &visited) {
int minimum = INT_MAX, min_index;
for (int i=0; i<V; i++) {
if (visited[i] == false && key[i] < minimum) {
minimum = key[i];
min_index = i;
}
}
return min_index;
}
void prim() {
vector<int> key(V, INT_MAX);
vector<bool> visited(V, false);
vector<int> parent(V);
key[0] = 0;
parent[0] = -1;
for (int i=0; i < V-1; i++) {
int u = minimum(key, visited);
visited[u] = true;
for (int v=0; v<V; v++) {
if (graph[u][v] && visited[v] == false && graph[u][v] < key[v]) {
parent[v] = u;
key[v] = graph[u][v];
}
}
}
printMST(parent);
}
void printMST(vector<int> &parent) {
cout << "Edge \tWeight\n";
for (int i=1; i<V; i++) {
cout << parent[i] << " - " << i << " \t" << graph[i][parent[i]] << endl;
}
}
int main() {
graph = { { 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 } };
prim();
}
Priority Queue
But the more efficient way is to go ahead and use priority queue!
#include<bits/stdc++.h>
using namespace std;
// Function to find sum of weights of edges of the Minimum Spanning Tree.
int spanningTree(int V, int E, vector<vector<int>> &edges) {
// Create an adjacency list representation of the graph
vector<vector<int>> adj[V];
// Fill the adjacency list with edges and their weights
for (int i = 0; i < E; i++) {
int u = edges[i][0];
int v = edges[i][1];
int wt = edges[i][2];
adj[u].push_back({v, wt});
adj[v].push_back({u, wt});
}
// Create a priority queue to store edges with their weights
priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>>> pq;
// Create a visited array to keep track of visited vertices
vector<bool> visited(V, false);
// Variable to store the result (sum of edge weights)
int res = 0;
// Start with vertex 0
pq.push({0, 0});
// Perform Prim's algorithm to find the Minimum Spanning Tree
while(!pq.empty()){
auto p = pq.top();
pq.pop();
int wt = p.first; // Weight of the edge
int u = p.second; // Vertex connected to the edge
if(visited[u] == true){
continue; // Skip if the vertex is already visited
}
res += wt; // Add the edge weight to the result
visited[u] = true; // Mark the vertex as visited
// Explore the adjacent vertices
for(auto v : adj[u]){
// v[0] represents the vertex and v[1] represents the edge weight
if(visited[v[0]] == false){
pq.push({v[1], v[0]}); // Add the adjacent edge to the priority queue
}
}
}
return res; // Return the sum of edge weights of the Minimum Spanning Tree
}
int main() {
vector<vector<int>> graph = {{0, 1, 5},
{1, 2, 3},
{0, 2, 1}};
cout << spanningTree(3, 3, graph) << endl;
return 0;
}
Above code is directly taken from Geek for Geeks.